So you go to the doctor and get a test for a disease, and they tell you the test is 99% accurate. Then the phone call comes, your test came back positive. What is the probability you have the disease? Chances are it's not 99%.
If a test is said to be 99% accurate what they are referring to is the probability of the test coming back positive if you do have the disease. What you are interested in is the probability of having the disease if your test comes back positive; these are not the same thing. With all things that are not 100% accurate there is a chance of a false positive, being told you are positive when you are not, and a false negative being told you are negative when you're not.
Let's assume the disease is fairly rare and only occurs in only 2% of a population. For a population of the size of Canada, 24 million, that means 480,000 people have it and 23,520,000 don't. Since our test is 99% accurate that means that of the people that are positive 475,200 will come back positive and only 4,800 will be be told they are not, ie a false negative. At the same time, of the people that are not positive 23,284,400 will be told they don't have the disease and 235,200 will be told they do.
This leaves percetage of people that are positive out of the number that are tested positive is 67%. Since the disease is so rare the number of false positives is almost half as much as the number of people who actually have the disease, this makes telling a false positive from a real one very difficult. The rarer the disease the worse this effect. In many cases a test like this is used to screen patients since although it may scare a few people, very few sick people slip through the system. From there they can perform more expensive accurate tests to determine the results for sure.
What do Statistics really mean? No pun intended. if it happens, or helps on average, why does it never happen to me. The statistics of every day life, and why sometimes they can make all the difference.
Thursday, June 2, 2011
Tuesday, May 24, 2011
If there's a 1 in 3 chance of winning, I'm guaranteed to win if I buy 3 tickets, right?
This year the Heart and Stroke Lottery had a 1 in 3 chance of winning. Actually they said 1 in 3, best odds ever. 1 in 3 is not actually an odds ratio, but the 1 to 2 odds are still the best odds ever. Odds are the ratio of wins to losses. Either way, technically there are 71,653 prizes and 250,000 tickets which are a 28.66% probability of winning, much less than the reported 33.33% chances of winning. But let us assume that the 1 in 3 is correct for the sake of simplicity. So you if bought 3 tickets at 1 in 3 odds you would have to win, right?
The probability of the first ticket wining is obviously 1 in 3. The probability of the second ticket winning is close to 1 in 3 but not exactly since the probability would have gone down in the first prize won, or up if it had not, but this is a tiny difference in 250,000 prizes so we'll ignore it. So by that the third ticket also has a 1 in 3 probability of winning. Since we are ignoring the effect of the missing tickets we are essentially assuming independence amoung the tickets, therefore we can multiply the three probabilities. That gives us that the probaility of just less than 4% of all three tickets winning. Which is not great, but it's not what we are looking for either.
So what about just winning one prize in 3 tickets. Well you do double your chances of winning, but those chances are still not that great. The probability of winning one or more prizes if you bought only three tickets = the probability of winning 1 or 2 or 3 prizes = 1- P(no prizes)=1-(2/3)^3. Which is about 70% chance of winning which is double the original 33.33%, but clearly not a guarantee. If you double the number of tickets to 6, then you get all the way to 91% chance of winning a single prize. Of course the only way to guarantee you will in a prize is to buy 178348 tickets, one more than the number of non-winning tickets.
But then again the fact that you are supporting a good cause changes the game completely. This way you get to donate money to a good cause, gamble (which is always fun), and get a tax break all in one. What could be better.
Monday, May 16, 2011
Gambling with Statistics vs Economics
I've heard a lot of colleagues say "As a statistician I cannot gamble", and they are completely right. As a statistician you should never gamble because statistically you will loose money on average. By that logic you can also never buy any type of insurance; in fact you could never really buy anything because on average you will loose money. What is important in all these situations is the utility or usefulness you get from the money you spent.
For instance if you buy a chocolate bar for a dollar you are loosing money in two ways, for the materials and for the labour. If you made it yourself it would cost a fraction of what you paid for it, but then again it would take time. Maybe to you an hour at your day job would make more money than the money you would save making a chocolate bar, so on balance you are saving money by paying for the time you saved.
When we gamble or buy something like insurance we are paying instead for pleasure or security (which in essence is a form of pleasure). Many things we pay for don't directly save us money like the chocolate bar but bring us pleasure and allow us to be more relaxed and therefore more productive, like going to a concert or playing a sport. Of course we can gain other types of utility from these activities lie networking and skills building, but they aren't really applicable to gambling. What it really comes down to is how much utility do you get from gambling? If you don't find it fun then don't go to the concert.
The main problem of gambling is when the utility of playing surpasses the actual value to a person. If gambling is the one thing that makes you the happiest spending some of your income is no worse than getting a pass to the ski hills or playing paintball. Money in, pleasure out, that makes it possible to make more money. But just like any activity, if it completely drains your account and leaves you with nothing it's an addiction and does nothing to boost your morale.
So what could be a better gift at christmas. Most children only spend a few minutes playing with most of their gifts anyway so why not buy them a lottery ticket. For many kids the thrill of a scratch ticket it equal if not more than a kinder egg, and they cost about the same, and that the lottery ticket has also a small probability of returning some or all of their money. Of course if you want a meaningful long lasting gift I would steer clear of the lottery tickets. It's all about the cost, is it worth it?
So instead of telling people how you don't gamble because it's statistically useless, tell them you take no pleasure out of gambling and therefore get no utility making it valueless to you. Because if some people didn't get pleasure out of gambling that first monkey would have never gambled leaving the trees in the first place
Tuesday, April 26, 2011
Some Statistics are poorly made, some are just poor
So what's wrong with this?
Nothing actually. Yes they have a selective sample, yes it's not random, but the population of interest that they are making an inference about is quite accurate.
At first glance it looks like Kellogg's is trying to pull a fast one and say that 100% of people love their cereal. However they are only saying that 100% of the people who like the cereal, like the cereal. It may sound stupid, but it is accurate. As for the in-depth statistical analysis, as long as they're collecting information about a sample it is a statistical analysis. In general we try to find deep understandings about the population from which the sample came, but who are we to judge.
Friday, March 4, 2011
How not to destroy the world
Does anyone else remember someone in the 90s saying something about the superpowers having enough nuclear arms to destroy the world "10 times over". Have you ever wondered if it's true.





So what does it mean to destroy the world really? Fortunately if you mean all of humanity that means we've got a lot of land to cover, all the oceans and all the land just to be sure. That's a whopping 510,072,000 square kilometers. That's a lot, trust me. So let's assume that if you're out at ocean during the apocalypse, it's too late for you, and if you're on an ice cap you've removed yourself from the gene pool anyway, crazy researchers :) Then there is only 148,940,000 square kilometers of land left, according to Wikipedia.

Ok, now onto the destruction. Although we all know the awesome power of the atomic bomb, they don't actually do all that much destruction in comparison to the world. Yeah, there's a radioactive dust cloud etc, but let's ignore that since it is really survivable. The largest ever exploded nuclear weapon was the Soviet Union's Tsar Bomb at 50 Megatons. At this size it is powerful enough to cause third degree burns at 100km, and light damage at 700km from the epicentre. Now not every bomb is a Tsar bomb, and actually most have significantly less yield. A number of sources including Encarta and wikipedia state a typical nuclear weapon causes moderate damage up to 24kms away.

Quantity has definitely decreased in recent years. Today there are less than 5,000 active warheads. If we expand it to the available inactive warheads as well there are a total of 20,000. So now we've got our quantity and maximum yield.
SO if we take the 148,940,000 square kilometers of land area divided by 20,000 bombs with a coverage of 24kms we get about 50% coverage. So it's not 10 times over, but it's not too shabby either, but that's only the land area. If we go to the full earth it's only 15%. Now of course we could target cities and so forth, but it's nice know that it's a pretty safe bet some people would survive in the nuclear apocalypse.
Sunday, February 27, 2011
Why do I always loose?
The good news is, you don't. Statistically everyone should win the same proportion of times.

A lot of it comes down to conformational bias. When a piece of toast is dropped it lands on the group butter side down 50% of the time, it's basically a coin (arguably it could be higher, but the difference is negligible). What happens though is that for many of the times that the bread lands buttered side down you pick it up and continue on your way without really noticing. On the other hand when it lands buttered side down it sucks. You make a big deal, quote the line, and have to clean it up.

I believe it anything is over 60% people notice it as an unfair coin. So when a few of the buttered side up are ignored it seems that the bread is favouring the buttered side more.

Now that doesn't mean you can't have a streak, even a really long one. Loosing or winning. Probabilistically it could happen for someone's entire life, although the it would be extremely rare, like one person ever, it's not you, don't worry. Even if you flip a coin 100 times you'd expect to see a string of head (or tails) at least 7 long.
When these streaks happen people often think they are lucky or cursed, but their luck will eventually turn, it's all in the numbers. The thing to remember is that the probability of each instance is fixed, it has nothing to do with anything before. Even though you got a string of 15 heads in a row, the probability on the next one is still 50%.

A lot of it comes down to conformational bias. When a piece of toast is dropped it lands on the group butter side down 50% of the time, it's basically a coin (arguably it could be higher, but the difference is negligible). What happens though is that for many of the times that the bread lands buttered side down you pick it up and continue on your way without really noticing. On the other hand when it lands buttered side down it sucks. You make a big deal, quote the line, and have to clean it up.

I believe it anything is over 60% people notice it as an unfair coin. So when a few of the buttered side up are ignored it seems that the bread is favouring the buttered side more.

Now that doesn't mean you can't have a streak, even a really long one. Loosing or winning. Probabilistically it could happen for someone's entire life, although the it would be extremely rare, like one person ever, it's not you, don't worry. Even if you flip a coin 100 times you'd expect to see a string of head (or tails) at least 7 long.
When these streaks happen people often think they are lucky or cursed, but their luck will eventually turn, it's all in the numbers. The thing to remember is that the probability of each instance is fixed, it has nothing to do with anything before. Even though you got a string of 15 heads in a row, the probability on the next one is still 50%.
Thursday, February 24, 2011
How the universe is "normally" distributed
On the average day, nothing is absolute. It's not exactly minus 5 degrees, the air isn't exactly one atmosphere, and gravity isn't even 1g. At any given time there's a random fluctionation around some central point. A distribution around a mean.

The easiest way to see it is when you're making a cake, or whipping cream. A single band forms around the middle of the bowl, with fewer and fewer specs out from the middle. If you were to plot the distribution of these points you would get something like this

This is called the Normal Distribution. This is what "normally" happens. Most things are around some central value, but everything is possible, it's just less and less likely the further you get from the middle. That's why there's whipped cream on your fridge. If you run the beeters for long enough, the one in a million chance can happen, and that rare value way off on the curve is far enough out to leave the bowl and go wizzing across the room to hit your fridge.This is the basis of a large part of statistics. As you can see the probability drops of very quickly. Something called the Empirical rule tells us that we should expect almost 70% of the values within one standard deviation, and a whopping 95% within 2 standard deviations. By the time we get 3 standard deviations out we covered 99.6% of all possible outcomes from the population.

This is how so called anomalies occur. The bulk of observations are pretty close to the middle, occasionally there are some that are slightly off the mean, but once in a blue moon (That's two moons in one month btw) truly crazy stuff happens. We call those outliers.

And although the formula for it is rather unpleasant you'll notice that both pi and e (a number like pi) and the square root of two are all part of it. For math types, this is deep. Potentially the three most impotant numbers in science all part of a formula that came out of everyday experience. Pretty awesome. So the next time something truly incredible and strange happens, just remember it's "normal".

The easiest way to see it is when you're making a cake, or whipping cream. A single band forms around the middle of the bowl, with fewer and fewer specs out from the middle. If you were to plot the distribution of these points you would get something like this
This is called the Normal Distribution. This is what "normally" happens. Most things are around some central value, but everything is possible, it's just less and less likely the further you get from the middle. That's why there's whipped cream on your fridge. If you run the beeters for long enough, the one in a million chance can happen, and that rare value way off on the curve is far enough out to leave the bowl and go wizzing across the room to hit your fridge.This is the basis of a large part of statistics. As you can see the probability drops of very quickly. Something called the Empirical rule tells us that we should expect almost 70% of the values within one standard deviation, and a whopping 95% within 2 standard deviations. By the time we get 3 standard deviations out we covered 99.6% of all possible outcomes from the population.

This is how so called anomalies occur. The bulk of observations are pretty close to the middle, occasionally there are some that are slightly off the mean, but once in a blue moon (That's two moons in one month btw) truly crazy stuff happens. We call those outliers.

And although the formula for it is rather unpleasant you'll notice that both pi and e (a number like pi) and the square root of two are all part of it. For math types, this is deep. Potentially the three most impotant numbers in science all part of a formula that came out of everyday experience. Pretty awesome. So the next time something truly incredible and strange happens, just remember it's "normal".
Wednesday, February 16, 2011
Calculating without a Calculator
Ever wonder how your grandparents ever survived math class? No I don't mean it's so hard noone could ever survive, and no math wasn't just really easy "back then". But how would someone do a complex mathematical computation without a calculator.

Yes there were slide rulers, but no, I mean before that. So how would one work out something simple like the square root of 71.
There was of course a much higher reliance on personal math skills, most students these days will use their calculator for simple addition. Oh we've all done it, "just to be sure". So that helped of course, things were much faster. But √71 is still hard. One thing we can do is guess. We know 8^2 is 64 and 9^2 is 81, so √71 is probably 8.4ish. We can then do 8.4^2 which 70.56, not big enough, but not by much, so let's try 8.45^2=71.4025, too big, And so on... It takes a while, and some good long multiplication, but it will work, and you can get as many decimals as you need. So there's the solution.
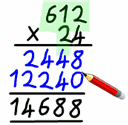
Let's say every day you and a bunch of people are doing this every day, then maybe we could higher someone to do it for you and do them ahead of time. Then evolved Table books. I picked one of these up a few years back called 6 place tables. Pages and pages of numbers. Want √71, go to the square root chapter, scroll to 71, there's your answer to 6 decimal places.

Now this of course only works for simple math, which for most math classes is enough, but what if you're doing higher level math. Well Roynald Fisher, One of the fathers of statistics, had a solution. He employed 30 women that work as his "Calculator". Monday morning, "Find the √37894.2389. Three people per computation then worked and compared ansers for accuracy.
So the next time you're annoyed with Math, just think about how much mathematical computing power you have in that dollar bin calculator. Anyone before 1900 would give their right arm for it.

Yes there were slide rulers, but no, I mean before that. So how would one work out something simple like the square root of 71.
There was of course a much higher reliance on personal math skills, most students these days will use their calculator for simple addition. Oh we've all done it, "just to be sure". So that helped of course, things were much faster. But √71 is still hard. One thing we can do is guess. We know 8^2 is 64 and 9^2 is 81, so √71 is probably 8.4ish. We can then do 8.4^2 which 70.56, not big enough, but not by much, so let's try 8.45^2=71.4025, too big, And so on... It takes a while, and some good long multiplication, but it will work, and you can get as many decimals as you need. So there's the solution.
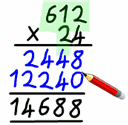
Let's say every day you and a bunch of people are doing this every day, then maybe we could higher someone to do it for you and do them ahead of time. Then evolved Table books. I picked one of these up a few years back called 6 place tables. Pages and pages of numbers. Want √71, go to the square root chapter, scroll to 71, there's your answer to 6 decimal places.

Now this of course only works for simple math, which for most math classes is enough, but what if you're doing higher level math. Well Roynald Fisher, One of the fathers of statistics, had a solution. He employed 30 women that work as his "Calculator". Monday morning, "Find the √37894.2389. Three people per computation then worked and compared ansers for accuracy.
So the next time you're annoyed with Math, just think about how much mathematical computing power you have in that dollar bin calculator. Anyone before 1900 would give their right arm for it.
84 different Burger Combinations Available!
Ever wondered what it would take to make say 80 different burgers? or 39 different ice cream flavours?Well in reality it doesn't take much, not having a any good taste helps. Furthermore it doesn't actually take that many toppings.

What we're looking at is a simple combination formula. Each ingredient can be combined with a certain number of ingredients to make a burger with say 4 toppings.
Where n is the number of available toppings, and r is the number of toppings on the burger. We can further simplify this to encompass all possible combinations, or all possible burgers. Since each topping can be either on or off the burger each topping takes one of two options. Multiple that by the two options of the next topping and you get
So a typical burger joint that offers tomatoes, lettuce, pickles, mustard, relish, mayo, ketchup, onions, cheese and bacon can make an astounding 1024 different burgers. The math is really that simple.

Ok so let's be fair, those are really condiments, and not really different burgers. However to be able to claim 80 different burgers we would only need 7 different fixings.
Similarly Baskin Robbins doesn't need much to claim 39 different flavours. Just Vanilla ice cream and some walnuts, chocolate chips, pecans, caramel and marshmallows makes 32 different flavours. So what we really need to do is measure the available ingredients to properly compare.

This ice cream shop I visited in Nice, France had everything from tomato, to bread, to rose ice cream. Just flavours nothing added, now that's impressive.

What we're looking at is a simple combination formula. Each ingredient can be combined with a certain number of ingredients to make a burger with say 4 toppings.
Where n is the number of available toppings, and r is the number of toppings on the burger. We can further simplify this to encompass all possible combinations, or all possible burgers. Since each topping can be either on or off the burger each topping takes one of two options. Multiple that by the two options of the next topping and you get
So a typical burger joint that offers tomatoes, lettuce, pickles, mustard, relish, mayo, ketchup, onions, cheese and bacon can make an astounding 1024 different burgers. The math is really that simple.

Ok so let's be fair, those are really condiments, and not really different burgers. However to be able to claim 80 different burgers we would only need 7 different fixings.
Similarly Baskin Robbins doesn't need much to claim 39 different flavours. Just Vanilla ice cream and some walnuts, chocolate chips, pecans, caramel and marshmallows makes 32 different flavours. So what we really need to do is measure the available ingredients to properly compare.

This ice cream shop I visited in Nice, France had everything from tomato, to bread, to rose ice cream. Just flavours nothing added, now that's impressive.
Monday, January 24, 2011
The Black Sheep
An Mechanical Engineer, a Physicist and a Mathematician are on a train going to a conference in Scotland . As they come out of a tunnel just entering Scotland the Engineer spots a sheep on a hill.
"hey look guys a Black sheep, I guess all sheep in Scotland are Black." says the Engineer
"No silly, just that one sheep is Black in Scotland," Says the Physicist.
"You're both wrong, always generalizing," says the Mathematician. "We only know there is one side of one sheep in Scotland that is black."
Friday, January 21, 2011
Let's make a deal
Back in the 1970s there was a game show called Let's Make a Deal, hosted by Monty Hall, which created quite a stir when statistics got involved.

The game show went like this. There are three doors; behind one of the doors is a brand new car (Or similarly nice prize) and behind the other two is a goat. And no you don't want a goat. The contestent is then asked to pick a door. Monty Hall would then "reveal" one of the two remaining doors to show one of the goats. This left two unopened doors.
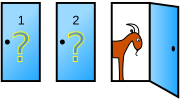
The challenge now is, "would you like to stay with the door you first chose, or switch to the other unopened door". The statistics question is; what is the probability that the other unopened door has the car behind it?

Initially people thought that it was a simple 50:50 bet. There are two doors, one has a car, one does not. But this is why we have statistics, to go beyond common sense and discover strange underlying probabilities. The real controversy started when Marilyn vos Savant's "Ask Marilyn" column in Parade magazine in 1990. She stated that one should always switch. Numerous readers including PhD's and respected statisticians wrote in to her "switch tactic was wrong. Here's why she is right.

Let's say you pick door number one. The probability the car is behind it is then 1/3, since one door has a car, and two have goats. Therefore the probability that the other two doors (2 or 3) contain the car is 2/3. When a goat is revealed to be behind door number 2, that probability does not change. Thee is still a 2/3 probability that the car is behind door number 2 or 3. Obviously don't pick 2, so the probability of door number 3 having the car is 2/3.
Seen another way. All possible setups of doors are (C=Car, G=Goat)

So if we switch our door in the first setup, we loose. If we change on the second we win, and the third we win. Therefore we wind 2/3 of the time. If you don't believe me here's a link to an applet, http://math.ucsd.edu/~crypto/Monty/monty.html. You can play the game until your hearts content, and as you'll notice, you'll win 2/3s of the time if you switch your door. Ain't Stats fun.

The game show went like this. There are three doors; behind one of the doors is a brand new car (Or similarly nice prize) and behind the other two is a goat. And no you don't want a goat. The contestent is then asked to pick a door. Monty Hall would then "reveal" one of the two remaining doors to show one of the goats. This left two unopened doors.

The challenge now is, "would you like to stay with the door you first chose, or switch to the other unopened door". The statistics question is; what is the probability that the other unopened door has the car behind it?

Initially people thought that it was a simple 50:50 bet. There are two doors, one has a car, one does not. But this is why we have statistics, to go beyond common sense and discover strange underlying probabilities. The real controversy started when Marilyn vos Savant's "Ask Marilyn" column in Parade magazine in 1990. She stated that one should always switch. Numerous readers including PhD's and respected statisticians wrote in to her "switch tactic was wrong. Here's why she is right.
Let's say you pick door number one. The probability the car is behind it is then 1/3, since one door has a car, and two have goats. Therefore the probability that the other two doors (2 or 3) contain the car is 2/3. When a goat is revealed to be behind door number 2, that probability does not change. Thee is still a 2/3 probability that the car is behind door number 2 or 3. Obviously don't pick 2, so the probability of door number 3 having the car is 2/3.
Seen another way. All possible setups of doors are (C=Car, G=Goat)
CGG
GCG
GGCIf we pick the first door, then Monty would open these doors

So if we switch our door in the first setup, we loose. If we change on the second we win, and the third we win. Therefore we wind 2/3 of the time. If you don't believe me here's a link to an applet, http://math.ucsd.edu/~crypto/Monty/monty.html. You can play the game until your hearts content, and as you'll notice, you'll win 2/3s of the time if you switch your door. Ain't Stats fun.
Tuesday, January 18, 2011
What is Probability
Probability is the likelihood that an event will happen, or has happened. In order to project into the future we pretend everything has happened and see what proportion were a success.

In everyday language we often express this as a percent and as most people has difficulty working with decimals. No other reason. 9 out of nine is 1 not 100%. While we're on the topic the conversion to percent should be written (9/9)% or (9/9)x100, not both. Per Cent means per 100, therefore (9/9)x100% is 1 times 100 per 100 which is 1. Try it on your calculator, 1 times 100 then %.

The way that we use percentages and probabilities also differ slightly in everyday language. We talk about percentages as the proportion of successes in the total, but a probability often refers proportion of times a single event will be a success.The meaning is just ever so slightly different, the result is the same often, but the path to get there is different.

In school we say that a test that got 13 out of 100 question right got 13%. And could have been written by a monkey guessing randomly. But that's wrong.... The bit about the monkey. No the monkey couldn't have guessed randomly, and certainly neither could a student, but that's another story. The 13% is right though. They got 13% of the questions right. But that doesn't really tell us anything, it just clumps all the data into one point. In probability we would say that, the probability of any particular question being right, is 13%. Let's think about that. I pick one question from the test there is a 13% change that it is right.

This shift in thinking is one of the first challenges made by all students takeling their first statistics course. Fundamentally we want to know the behaviour of a given individual. But we can only determine this by figuring out the behaviour of the entire population and hoping that the individual will land near an "average" individual from the population. Once you get past this many of the "calculations" of higher order probabilities are quite simple.

If I roll 2 dice, what is the probability that one is a 4 given that they add to 9. "Not a clue, no idea where to start." Well think about one instance, and start with what we know. We know they add to 9, therefore the dice must be one of– 4,5; 5,4; 6,3; 3,6. That's 4 different pairs. Which ones of them have a 4; two of them. Therefore the probability that one is a 4 given that they add to 9 is 2/4, or one half.

How does this relate? What we did differently here was to look at the individual in order to extrapolate. So just like the test, instead of looking at one question and trying to guess the probability if will be right, we looked at every one, determined the probability of a correct answer on average, then the probability of a success for that individual should be the same.

And this applies to all of statistics. Every statistics problem is simply determining the number of successes and failures in every possible outcome in order to determine the probability of a single success on a single individual, and sometimes we've come up with nice formulae to make quick calculation shortcuts. It's all the same. Determine every single possibility, figure out how many of them are successes, successes out of total equal probability.
And that's probability.

In everyday language we often express this as a percent and as most people has difficulty working with decimals. No other reason. 9 out of nine is 1 not 100%. While we're on the topic the conversion to percent should be written (9/9)% or (9/9)x100, not both. Per Cent means per 100, therefore (9/9)x100% is 1 times 100 per 100 which is 1. Try it on your calculator, 1 times 100 then %.
The way that we use percentages and probabilities also differ slightly in everyday language. We talk about percentages as the proportion of successes in the total, but a probability often refers proportion of times a single event will be a success.The meaning is just ever so slightly different, the result is the same often, but the path to get there is different.

In school we say that a test that got 13 out of 100 question right got 13%. And could have been written by a monkey guessing randomly. But that's wrong.... The bit about the monkey. No the monkey couldn't have guessed randomly, and certainly neither could a student, but that's another story. The 13% is right though. They got 13% of the questions right. But that doesn't really tell us anything, it just clumps all the data into one point. In probability we would say that, the probability of any particular question being right, is 13%. Let's think about that. I pick one question from the test there is a 13% change that it is right.

This shift in thinking is one of the first challenges made by all students takeling their first statistics course. Fundamentally we want to know the behaviour of a given individual. But we can only determine this by figuring out the behaviour of the entire population and hoping that the individual will land near an "average" individual from the population. Once you get past this many of the "calculations" of higher order probabilities are quite simple.

If I roll 2 dice, what is the probability that one is a 4 given that they add to 9. "Not a clue, no idea where to start." Well think about one instance, and start with what we know. We know they add to 9, therefore the dice must be one of– 4,5; 5,4; 6,3; 3,6. That's 4 different pairs. Which ones of them have a 4; two of them. Therefore the probability that one is a 4 given that they add to 9 is 2/4, or one half.

How does this relate? What we did differently here was to look at the individual in order to extrapolate. So just like the test, instead of looking at one question and trying to guess the probability if will be right, we looked at every one, determined the probability of a correct answer on average, then the probability of a success for that individual should be the same.

And this applies to all of statistics. Every statistics problem is simply determining the number of successes and failures in every possible outcome in order to determine the probability of a single success on a single individual, and sometimes we've come up with nice formulae to make quick calculation shortcuts. It's all the same. Determine every single possibility, figure out how many of them are successes, successes out of total equal probability.
And that's probability.
Monday, January 10, 2011
Standard Deviation Explained
One of the best things about statistics is that it's not really that old as a science. The language that is used is fairly recent, kind of an old english stodginess to it. Most terms just have to be taken back to their strict dictionary definition to be understood. So standard deviation simply means, The Standard... Deviation.

You know both of these words, we just don't tend to use them a lot in every day language. At least not together, or in this way. The American Oxford Dictionary defines standard, as

Now, we often hear deviation in one of its variants; deviate or deviant. "You deviated from what you were told," meaning not quite correct. Or, "they're a social deviant", meaning unacceptable. So deviation means something has changed from what was expected. Together they give us,

If you take the whole data set, and take the average difference between each point and what is expected you get the standard deviation. In statistics this is often reported as a single value and will have the same units as the expected value. For instance, men in Canada are 1.736 m on average with a standard deviation of 16cm (Made this up, I still can't find it). That means that the average Canadian male height is on average 16cm from 1.736 m. Yes this tells you nothing about the individual person, or what you might expect to see in a small group, but it does tell you information about all Canadians in general.

You know both of these words, we just don't tend to use them a lot in every day language. At least not together, or in this way. The American Oxford Dictionary defines standard, as
Standard: used or accepted as normal or average : the standard rate of income tax | it is standard practice in museums to register objects as they are acquired.Something that you expect to have happen, or what you would expect to see on Average. Let's go with that, the average.
Now, we often hear deviation in one of its variants; deviate or deviant. "You deviated from what you were told," meaning not quite correct. Or, "they're a social deviant", meaning unacceptable. So deviation means something has changed from what was expected. Together they give us,
The Average Change from the Expected.

If you take the whole data set, and take the average difference between each point and what is expected you get the standard deviation. In statistics this is often reported as a single value and will have the same units as the expected value. For instance, men in Canada are 1.736 m on average with a standard deviation of 16cm (Made this up, I still can't find it). That means that the average Canadian male height is on average 16cm from 1.736 m. Yes this tells you nothing about the individual person, or what you might expect to see in a small group, but it does tell you information about all Canadians in general.
Friday, January 7, 2011
The statistics of un-reportable data
According to Stockwell Day says unreported crimes are rising Statistics Canada reported that only 34% of Victims of Crime reported to the police. You ever wonder how they know that? Like really? If the crime goes unreported, how could we make a statistic based on it?

Well yes, there is Big Brother, and of course eye witness accounts, but those would might be put under reported crime. One way is to have a blind survey where there is an assurance that the answers cannot be linked to the surveyor, something like the Canadian Census. Oh wait, the old Canadian Census. The new one couldn't tell you... well anything. Either way, people are asked to recount any crime they've been a part of, as victim or criminal, along with the date, then these statistics are matched up with current crime rate data, and any discrepancy is assumed to be the unreported portion. But that leaves one major question. What is the variance?

Now anybody can make up any statistic by simply using ANY data set. It's a perfectly valid statistical procedure. For instance, I could use the shrub in my front yard to estimate the average height of people in Canada. Nothing wrong with that. "I think people in Canada are 12ft tall on average." This in not wrong, it's an estimate. What we assume when we hear a statistic from a body like Statistics Canada though, is that the Variance, or general variability of the statistic is small. My shrub estimator for instance probably has a variance of about 100ft. That is, people in Canada are on average 12ft tall give or take 100ft. Woowee, that's really helpful, people are between 0 and 112ft tall (assumed nobody has a negative height).
And that's what you should ask yourself with the unreported crime data set. Yes there are only 34% of crimes reported, but plus or minus what. Unfortunately very few statistics in the news are reported with standard deviation (the statistical term for variability), or even any sort of hint as to how accurate the measure even is. I, for example, can't find the standard deviation of male heights in Canada to save my life (If you find one please comment, first one gets a free lolli).

Since the crime estimate is probably based on a survey, one would need to know the sample size and reliability of the survey to really get an idea of how good a number it is. People wouldn't necessarily put down crime, so it may even be unreported. Although negative statistics like crime are often inflated to compensate. Also the demographic coverage would be key. If you live in Northern Ontario you wouldn't expect the percentage of unreported crime to be the same as manhattan. Or would you? So in the end it all comes down to extrapolation and what the data is based on. How far can I stretch the claim about this data, and is their situation anything like mine.

Well yes, there is Big Brother, and of course eye witness accounts, but those would might be put under reported crime. One way is to have a blind survey where there is an assurance that the answers cannot be linked to the surveyor, something like the Canadian Census. Oh wait, the old Canadian Census. The new one couldn't tell you... well anything. Either way, people are asked to recount any crime they've been a part of, as victim or criminal, along with the date, then these statistics are matched up with current crime rate data, and any discrepancy is assumed to be the unreported portion. But that leaves one major question. What is the variance?

Now anybody can make up any statistic by simply using ANY data set. It's a perfectly valid statistical procedure. For instance, I could use the shrub in my front yard to estimate the average height of people in Canada. Nothing wrong with that. "I think people in Canada are 12ft tall on average." This in not wrong, it's an estimate. What we assume when we hear a statistic from a body like Statistics Canada though, is that the Variance, or general variability of the statistic is small. My shrub estimator for instance probably has a variance of about 100ft. That is, people in Canada are on average 12ft tall give or take 100ft. Woowee, that's really helpful, people are between 0 and 112ft tall (assumed nobody has a negative height).

And that's what you should ask yourself with the unreported crime data set. Yes there are only 34% of crimes reported, but plus or minus what. Unfortunately very few statistics in the news are reported with standard deviation (the statistical term for variability), or even any sort of hint as to how accurate the measure even is. I, for example, can't find the standard deviation of male heights in Canada to save my life (If you find one please comment, first one gets a free lolli).

Since the crime estimate is probably based on a survey, one would need to know the sample size and reliability of the survey to really get an idea of how good a number it is. People wouldn't necessarily put down crime, so it may even be unreported. Although negative statistics like crime are often inflated to compensate. Also the demographic coverage would be key. If you live in Northern Ontario you wouldn't expect the percentage of unreported crime to be the same as manhattan. Or would you? So in the end it all comes down to extrapolation and what the data is based on. How far can I stretch the claim about this data, and is their situation anything like mine.
Subscribe to:
Posts (Atom)












